2022年08月23日

Introduction

“The fundamental problem of communication is that of reproducing at one point either exactly or approximately a message selected at another point.”

A mathematical Theory of Communication, an article published in the middle of the last century by mathematician Claude E. Shannon while working at Bell Labs, laid out the foundation of how modern society understands communication, that is, through the lens of Information Theory.

The standard definition of information theory is disappointingly circular; it has to do with the scientific study of the transmission, processing, and storage of information through mathematics. One question that emerges naturally after facing this definition is what exactly is information? which is exactly the question I’m going to tackle in the following post.

Information as a measure of uncertainty

“[…] the actual message is one selected from a set of possible messages. […] If the number of messages in the set is finite then this number or any monotonic function of this number can be regarded as a measure of the information produced when one message is chosen from the set […].”

Let’s start with something simpler than the fundamental communication problem by asking ourselves how surprised would we be if a coin lands on tails after flipping it?

Shannon’s first contribution to the understanding of information was to settle how it should be quantified; intuitively, the more information we have about the outcome of a random event (e.g. tossing a fair coin), the less surprised we will be after that event indeed occurred (e.g. the coin lands on tails). This suggests that “the surprising factor” of the outcome of a random variable should be a monotonicly decreasing function of its amount of information. Also, note that a maximally probable event (i.e. an event with probability \(1\)) will yield no surprise at all!

Meet the logarithmic measure of information, also known as self-information:

\[I(x) := -\log p(X = x)\]

where \(p(X = x)\) is the probability of the outcome \(x\). If the base of the logarithm function is \(2\). Self-information tells us the information content associated with an outcome of a random process.

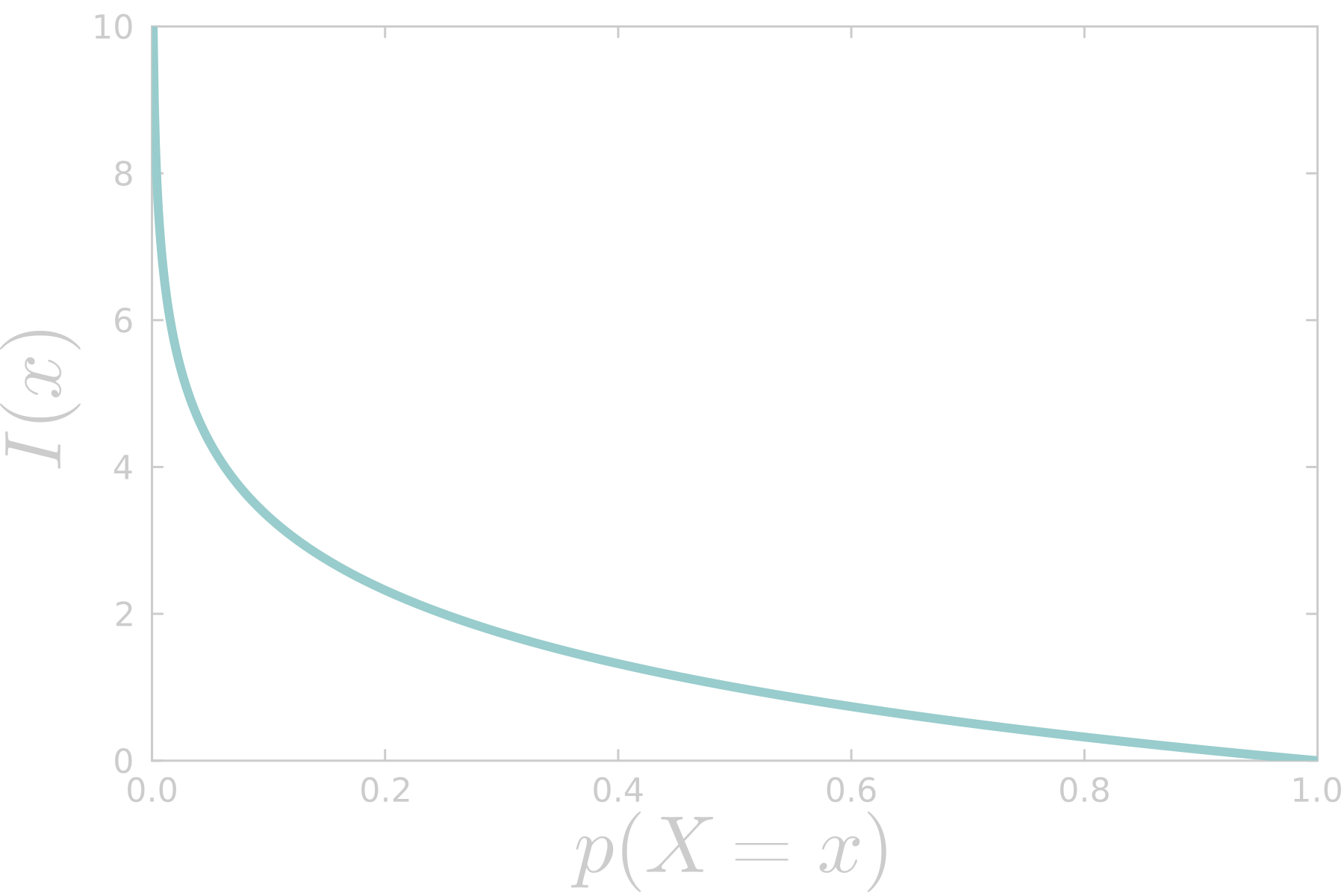
Now we know we would be just a bit surprised if a coin lands on tails (\(T\)) after flipping it, since the self-information of that outcome is \(1\) bit:

\[\begin{aligned} I(p(T)) &= - \log_2 p(T)\\ &= - \log_2 (0.5)\\ &= 1 \ \text{bit} \end{aligned}\]

Furthermore, we could ask whether we would be more surprised by winning the lottery (\(W\)) or by having a coin landing on heads (\(H\)), \(I(p(W)) \gt I(p(H))\). Assuming that the probability of winning the lottery is \(p(W) = 0.0000000715\) we can compute the self-information for this outcome:

\[\begin{aligned} I(p(W)) &= - \log_2 p(W)\\ &= - \log_2 (0.0000000715)\\ &\approx 24 \ \text{bit} \end{aligned}\]

Of course, we would be more than a bit surprised by winning the lottery! The surprise factor is equivalent to our uncertainty about the outcome of an event, it’s just a matter of occurrence. The bottom line is, that the more self-information we have over the outcome of a random variable, the more uncertain we are about it, and the more surprising will be that outcome.

So far we have explored the information contained in the outcome of a random event (i.e. self-information), but as we will see in a moment, most of the time is more interesting to ask ourselves What event is more surprising on average? is it flipping a coin where both outcomes have the same probability?, or playing the lottery where one outcome is very unlikely while the other wouldn’t surprise us at all.

Entropy

The average “surprising factor” over all the possible outcomes of a random event (i.e. the expected value of self-information) is known as Information Entropy (\(H\)):

\[H(X) := - \sum_{x \in X} p(X = x) \log p(X = x)\]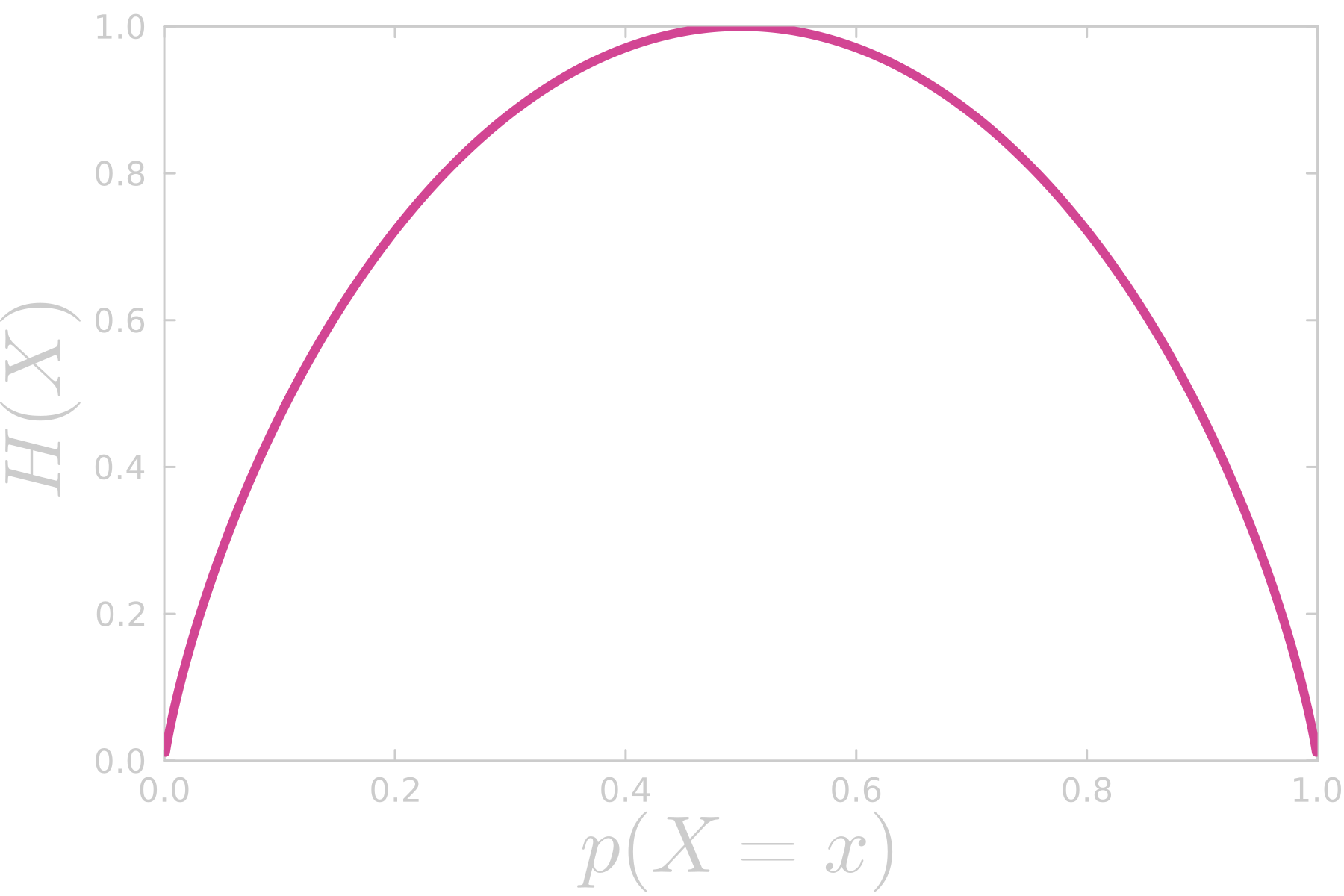

\(H(X)\) is all we need to answer our previous question; the entropy of flipping a fair coin is:

\[\begin{aligned} H_c &= - (p(H) \log_2 p(H) + p(T) \log_2 p(T))\\ &= 1 \ \text{bit} \end{aligned}\]

while the entropy associated with playing the lottery is:

\[\begin{aligned} H_l &= - (p(L) \log_2 p(L) + p(W) \log_2 p(W))\\ &\approx 0.0000018 \ \text{bit} \end{aligned}\]

As we can also infer from the figure above, on average, we gain much more information (and we’d be more surprised) with the outcomes of tossing a fair coin than the outcomes of playing the lottery.

Entropy tells us how spread out a probability distribution is. To illustrate this point, first consider a discrete uniform distribution with probability mass function:

\[u(x;a, b) = \frac{1}{b - a + 1}\]

where \(a, b\) are integers with \(b \geq a\). Let \(N = b - a + 1\), the support of the distribution, and compute the information entropy of the resulting distribution:

\[\begin{aligned} H(X) &= - \sum_{x \in X} u(x) \log u(x)\\ &= - N \frac{1}{N} (\log 1 - \log N)\\ &= log N \end{aligned}\]

Secondly, consider the same probability distribution (i.e. Bernoulli’s) we have been implicitly using for calculating the probability of having a particular binary outcome of a random event:

\[b(k;p) = \begin{cases} p \ \text{if} \ k = 1\\ 1 - p \ \text{if} \ k = 0\\ 0 \ \text{otherwise.} \end{cases}\]

And compute its entropy as well:

\[\begin{aligned} H(K) &= - \sum_{k \in K} b(k) \log b(k)\\ &= - (1-p) \log (1-p) - p \log p \end{aligned}\]

Note that \(H(X) \gt H(K)\), furthermore, it happens to be the case that the information entropy of a uniformly distributed random variable will be higher than the entropy of a random variable distributed otherwise.

Reference

YT channel Computerfile’s video on Why Information Theory is Important